Dartsで事前予約を加味した時系列の需要予測をしてみる

はじめに

今回は、事前予約型の乗車サービスにおける乗車需要を時系列解析を用いて予測します。ポイントとなるのが、注文日時と乗車日時の間に数日間のラグがあることです。典型的には、過去の乗車実績の時系列の変動から未来のそれを予測します。事前予約型ではさらに、事前に注文された乗車予定のデータを加味することが効果的であると考えられます。ここでは、シミュレーションによって事前予約型の注文のトイデータを作成し、事前予約を加味した時系列モデルを構築し検証します。また、同じモデルで実際のデータでの検証結果の概要も示します。

時系列解析を行うにあたっては、DartsというPythonのライブラリを利用しました。統計的手法や機械学習含め多数の時系列解析の予測モデルが備え付きで利用できます。そして、時系列データに対する様々な操作、モデルの構築・検証などが、統一的なAPIを通して利用できます（参考１、参考２）。コード断片を通してこちらも紹介できればと思います。なお、今回利用した一連のコードはこちらに公開しています。

乗車実績のトイデータ作成

まず、乗車日時の確率分布が、週毎、月毎、四半期毎に周期的になるようにして、乗車日時のリストをランダムに生成します。

from darts.utils.timeseries_generation import sine_timeseries, constant_timeseries
time_length = 365
sample_size = 10000
distribution = sum([
    sine_timeseries(length=time_length, value_frequency=(4/365), value_y_offset=1, freq='D'),
    sine_timeseries(length=time_length, value_frequency=(1/30), value_y_offset=1, freq='D'),
    sine_timeseries(length=time_length, value_frequency=(1/7), value_y_offset=1, freq='D'),
    constant_timeseries(length=time_length, value=1, freq='D')])
p_values = (distribution / distribution.sum()[0]).values()[:,0]
times = distribution.time_index.values
ride_start_dates = np.random.choice(times, size=sample_size, replace=True, p=p_values)

そして、それを日毎に集計します。この時系列のデータはTimeSeriesとして格納します。

from darts import TimeSeries
time_counts = dict(zip(times, np.zeros(times.shape)))
uniuqe, counts = np.unique(ride_start_dates, return_counts=True)
for time, value in zip(uniuqe, counts):
    time_counts[time] = value
target_series_df = pd.DataFrame(data=time_counts.items(), columns=['time', 'count'])
target_series = TimeSeries.from_dataframe(target_series_df, freq='D', time_col='time', value_cols='count')

図にプロットします。

target_series.plot()

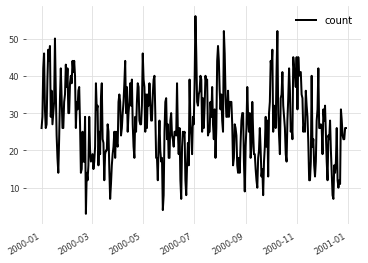
ノイズがありながらも指定した周期性があるのが分かります。

シンプルな予測

• モデルの構築

ここでは、素朴な時系列モデルとして指数平滑化法（ExponentialSmoothing）を利用します。Dartsの内部的には、ホルト-ウィンターズ法という"時系列の変動にトレンドと季節変動を追加し、それぞれの指数平滑の重ね合わせを期待値として算出する方法"を利用しています（参考）。

from darts.models import ExponentialSmoothing
model = ExponentialSmoothing()

• 学習と予測

ある時点でトレーニング用とテスト用のデータに分割し、トレーニングデータからモデルを学習し、テストデータの予測をします。

split_ts = pd.Timestamp('2000-11-01')
train, val = target_series.split_after(split_ts)
model.fit(train)
prediction = model.predict(len(val))

次の図はその結果で、実測値（target）と予測値（forecast）をプロットしたものです。

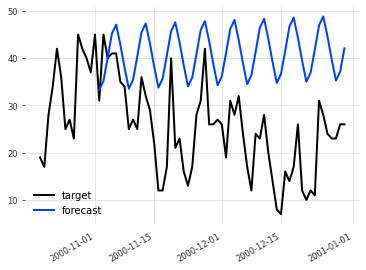
テスト期間の初期は比較的予測が合ってますが、時間とともにズレが大きくなっているのが見てとれます。

• バックテスト

時系列解析における予測精度を定量的に評価するため、バックテストという方法で検証します。 これは、時系列に沿った各時刻ステップにおいて、その時点までのデータを用いて学習したモデルを用いて、特定時刻ステップ先の値を予測していきます。

backtest = model.historical_forecasts(
    series=target_series, 
    forecast_horizon=forecast_horizon, 
    start=split_ts - Timedelta(timedelta(days=forecast_horizon)))

ここで、"forecast_horizon"は何時刻ステップ先（今回の場合は何日先）を予測するかという予測期間を指定します。"start"は予測を始めるタイミングを指します（ここではバックテストで予測された期間を揃えるため、"forecast_horizon"毎に"start"をずらしています）。

次の図は、予測期間を1日先と10日先にして予測したものです。

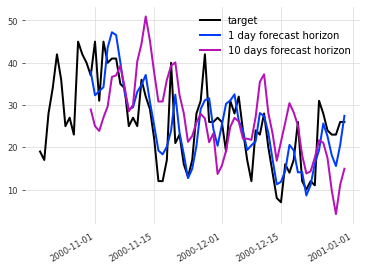
"1 day forecast horizon"はバックテストにおける1日先の予測、"10 days forecast horizon" は10日先の予測のプロットです。1日先の方が実測データによりフィットしているのが分かります。

バックテストで得た予測データと実測データとの誤差を表す指標として平均二乗偏差（RMSE）を用います。この値が小さいほど予測の精度が高いことを意味します。

from darts.metrics import rmse
print('Backtest RMSE = {}'.format(rmse(target_series, backtest)))

平均二乗偏差は、予測期間が1日と10日の場合それぞれ、5.88と10.75となり、1日先の予測の方が精度が高いことが伺えます。

• ベースラインモデルとの比較

先ほどのモデルが自明でない時系列の構造を捉えていることを示すため、もっとプリミティブなベースラインモデルと比較します。ここでは単に学習データの最後の値をそのまま以降の予測値として使用するものを用います。

from darts.models import NaiveSeasonal
model = NaiveSeasonal(1)

次の図は、先の指数平滑化法とベースラインのそれぞれのモデルにおいて、バックテストで算出した平均二乗偏差を予測期間に対してプロットしたものです。

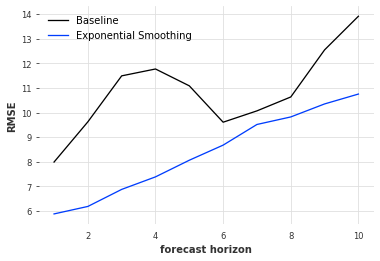
どの予測期間でも指数平滑化法がベースラインモデルよりも平均二乗偏差が小さい=予測精度が高くなっているのが分かります。なお、週単位の周期性があるため、予測期間が7日辺りでベースラインモデルの精度も高くなっています。

乗車予定のトイデータ作成

予測期間毎に、予測期間先の乗車予定のデータを作成します。

そのためにまず、先ほど生成した乗車日時のリストの各要素に対して、乗車日時と注文日時の差を生成します。差の分布は指数関数に従うようにします。

advanced_diffs = np.random.exponential(5, size=len(ride_start_dates))

こちらがそのヒストグラムです。

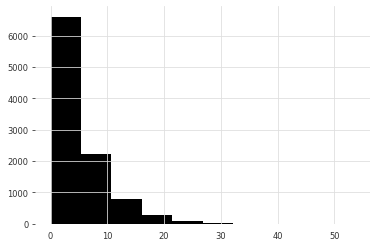
そして、注文日時と乗車日時の差が予測期間（＋集計タイミング）以上のもので乗車日時のリストをフィルタし、乗車時刻に関して日別にカウントします。

def get_advanced_series(forecast_horizon):
    advanced_start_dates = ride_start_dates[np.where(advanced_diffs >=  forecast_horizon + 1)]
    time_counts = dict(zip(times, np.zeros(times.shape)))
    uniuqe, counts = np.unique(advanced_start_dates, return_counts=True)
    for time, value in zip(uniuqe, counts):
        time_counts[time] = value
    advanced_series_df = pd.DataFrame(data=time_counts.items(), columns=['time', 'count'])
    advanced_series = TimeSeries.from_dataframe(advanced_series_df, freq='D', time_col='time', value_cols='count')
    return advanced_series

次の図は、１日先の乗車予定（"1 day advanced"）と１０日先の乗車予定（"10 days advanced"）のデータを実績データとともにプロットしたものです。

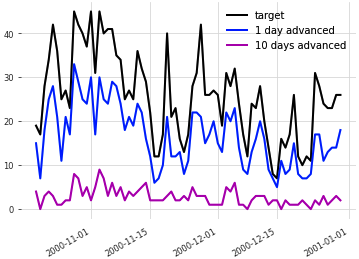
１日先の乗車予定の方が１０日先の乗車予定より、実績データに近づいていることが分かります。とはいえ、１０日先の乗車予定も兆候のようなものは見られます。

事前予約を加味した予測

• モデルの構築

今回は、事前予約を加味した時系列モデルとして、線形回帰（Linear Regression）を用いました。実績データと予定データからなる複数の変数から予測したい時点の実績値を回帰します。モデルの概要は次のようになります。

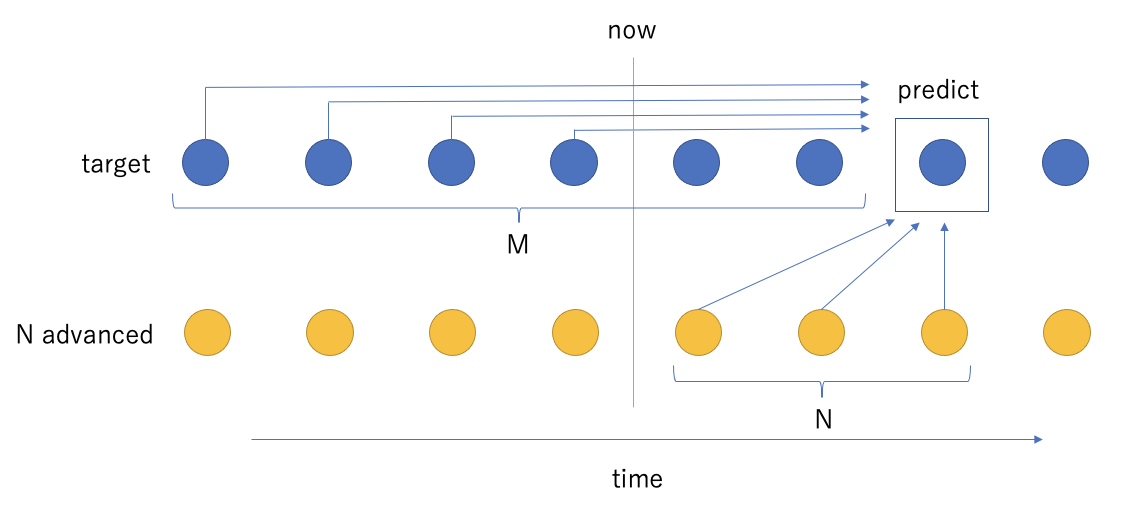
"target"は実績データ、"N advanced"はN日先の乗車予定データです。N日先の実績値を予測するため、未来のN点の乗車予定データと、予測点（"predict"）からM点前から現在（"now"）までの実績データを用います。これらを時系列に沿って取得しモデルを学習させます。ただし、N毎に別々のモデルを作成します。

コードとしてはこのような形になります。

from darts.models import RegressionModel
model_N = RegressionModel(lags=list(range(-M, 1 - N)), lags_future_covariates=list(range(1 - N, 1)) )

"lags"は予測点に対して実績データを学習に利用する際の期間、"lags_future_covariates"は予定データを学習に利用する際の期間です。"future_covariates"は未来に関する情報の変数で、例えば、天気予報の雨量などを設定します（参考）。

• モデルの評価

こちらもバックテストにより評価します。

backtest = model_N.historical_forecasts(
    series=target_series,  
    future_covariates=get_advanced_series(N),
    forecast_horizon=1, 
    start=split_ts - Timedelta(timedelta(days=1))

今回は、"future_covariates"としてN日先の乗車予定データを指定します。また、学習は予測点を起点とした時系列のインデックスになっているので"forecast_horizon"は1としています。

次に、平均二乗偏差を予測期間に対してプロットします。比較のため他のモデルによるものも加えました。

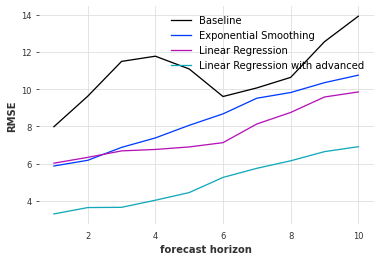
"Linear Regression with advanced"は事前予約を加味した線形回帰のモデル、"Linear Regression"は"future_covariates"を考慮しないで線形回帰を行ったものです。"Exponential Smoothing"と"Baseline"はそれぞれ、先ほどの指数平滑化法とベースラインモデルによるものです。事前予約を加味した線形回帰のモデルがどの予測期間に対しても最も低い平均二乗偏差=最も高い予測精度になっていることが分かります。

• 実際のデータでの評価

最後に、ある条件で抽出した実際の注文データに対して同様の解析を行なったものを示します。具体的には示しませんが、実際のデータ分布は上記のトイデータとある程度似たものとなっています。

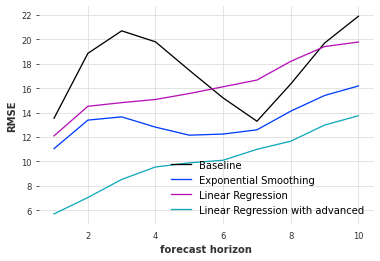
図の通り、トイデータと同様に、実際のデータに対しても事前予約を加味した線形回帰のモデルが最も高い予測精度になりました。

その他のモデル

公開したコードでは、線形回帰のモデルの他に、非線形な回帰手法として勾配ブースティングの一つであるLightGBMによる方法も検証しました。結果として、今回のデータでは線形回帰の方がわずかながら予測精度が高かったです。時間的に局所的な部分の線形性が強いためと推察されます。

また、曜日の情報を（sin/cosで符号化して）加味したモデルも構築して検証しました。結果は、曜日を考慮することでわずかながら予測精度が高まりました。特に、予測期間が1週間以降の方が曜日による効果が大きかったです。明示的な周期性の情報が予測に効いていると思われます。

他、Dartsにはニューラルネットワーク系のモデルも多数用意されていますが、今回はスコープ外としました。計算時間がかかるのとパラメタ調整が難しいので手軽には試せないのと、こちらはより大量で複雑なデータに対して威力を発揮するものと考えられるからです。

おわりに

事前予約型の乗車注文データに対して時系列解析を行い、事前予約の情報を加味したモデルの方が乗車需要を高い精度で予測できることを示しました。また、Dartsを用いてこのような解析が手軽に行えることを示しました。サービス開発において様々な場面で過去データから未来を予測することは重要です。今回の解析がその足掛かりなればと思います。

最後になりますが、NearMeではエンジニアを募集しています！まだまだ多くの可能性が潜んでいる領域です。興味を持った方はぜひ以下から応募いただければと思います。

• 採用サイトはこちら

Author: Kenji Hosoda